Scope of Morphology Study of Gravitation with Special Reference to Einstein’s Field Equation in General Relativity
Introduction
The concept of morphology in physics refers to the study of forms, structures, and their interrelationships across natural phenomena. While morphology is traditionally rooted in biology and anatomy, its adaptation into physical sciences provides a structural and geometrical perspective. When applied to gravitation, morphology allows us to understand the “shape” and “geometry” of spacetime, particularly through the lens of Einstein’s general theory of relativity. Gravitation is not merely a force, as once proposed by Newton, but a manifestation of spacetime curvature. Thus, morphology offers a conceptual framework to analyze how the geometry of spacetime evolves, distorts, and interacts with mass-energy distributions.
Morphological Scope of Gravitation
- Geometric Foundation of Gravity
- Morphology enables the visualization of gravity as curvature in spacetime rather than as an invisible force.
- Concepts such as geodesics, Riemannian curvature tensors, and metric tensors provide the “structural anatomy” of gravitational phenomena.
- Spacetime Structures and Forms
- Morphology highlights gravitational singularities, black holes, and event horizons as unique structural entities.
- Gravitational waves, ripples in spacetime, can be studied morphologically as oscillations of the cosmic fabric.
- Comparative Framework
- Just as biological morphology compares structures across species, gravitational morphology compares spacetime structures across different mass-energy distributions (stars, galaxies, black holes, and the early universe).
- Applications in Cosmology
- Morphological approaches extend to the large-scale structure of the universe, explaining galaxy clustering, cosmic web filaments, and voids.
Einstein’s Field Equation and Morphological Analysis
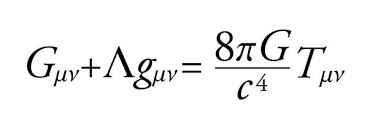
Einstein’s field equation is the cornerstone of general relativity:
- Morphological Interpretation:
- The left-hand side (geometry) represents the structural curvature of spacetime.
- The right-hand side (energy-momentum tensor) represents the distribution of matter and energy shaping that structure.
- Morphology thus provides a bridge between form (geometry of spacetime) and content (matter-energy).
- Structural Features Studied Morphologically:
- Singularities: points where curvature becomes infinite, akin to morphological “extremes.”
- Cosmic topology: large-scale shape of the universe.
- Black hole morphology: event horizon geometry, spacetime “throat” in wormholes.
Scope in Modern Physics
- Astrophysical Applications
- Understanding the morphology of neutron stars, black holes, and gravitational lensing.
- Cosmological Structures
- Morphological study of cosmic microwave background anisotropies, galaxy morphology, and dark matter clustering.
- Gravitational Waves
- Morphology helps describe waveforms and the structural dynamics of spacetime distortions.
- Quantum Gravity Prospects
- Future theories like string theory and loop quantum gravity rely on analyzing the micro-morphology of spacetime fabric.
Conclusion
The scope of morphological study of gravitation is vast, extending from the mathematical elegance of Einstein’s field equations to the structural interpretation of cosmic entities. By treating gravitation as a matter of form and structure, morphology provides a unifying perspective that connects geometry, matter, and cosmology. Einstein’s general relativity, with its emphasis on the geometry of spacetime, perfectly exemplifies the morphological nature of gravity.
